El teorema de Pitágoras es, posiblemente, la puerta de entrada para millones de personas al fascinante universo de la geometría y el razonamiento lógico. Debemos entender que este teorema no es solo una regla rígida, sino una relación profunda entre los lados de una figura que define nuestro espacio físico.
Su influencia fue tan vasta que los ecos de su escuela aún resuenan en las matemáticas modernas. Para cualquier matemático actual, la relación que planteó este sabio sigue siendo la piedra angular para calcular distancias y entender la semejanza entre formas complejas.
Si quieres conocer a otros visionarios que, al igual que él, transformaron el mundo con sus mentes, te invitamos a descubrir la historia de otros grandes científicos que marcaron un antes y un después.
¿Quién es Pitágoras?
Para entender su impacto, debemos retroceder hasta el siglo VI a.C. Si nos preguntamos hoy quién es Pitágoras, debemos imaginarlo como mucho más que alguien que sabía hallar el valor de una hipotenusa; fue un filósofo, un líder espiritual y un místico.
Nacimiento
Nacido en la Isla de Samos, Grecia
Lugar de la muerte
Metapontum Village, Italia
Viajes
se dice que viajó extensamente por Egipto y Babilonia donde absorbió conocimientos astronómicos y geométricos milenarios antes de fundar su propia escuela en Crotona, al sur de Italia.
En la Pitágoras historia se destaca la creación de la "Hermandad Pitagórica", una organización que mezclaba la ciencia con un estilo de vida ascético y ritualista. Para ellos, cada número no era una simple herramienta de conteo, sino la esencia misma de la divinidad y la realidad. Esta visión permitió que su escuela realizara avances tan disruptivos, analizando desde un simple polígono hasta la estructura misma del cosmos.
El matemático griego estableció que la naturaleza podía ser descifrada mediante una ecuación lógica.
Si sientes que necesitas una guía para navegar por estos conceptos históricos y numéricos, siempre puedes profundizar en matematicas con la ayuda de expertos que te expliquen cómo estas ideas antiguas siguen vivas hoy.
Aportes de Pitágoras a la matemática
Los aportes de Pitágoras a la matemática son tan numerosos que es difícil catalogarlos todos sin maravillarse.
Su escuela fue pionera en la teoría de números
clasificándolos en pares, impares y primos.
uno de sus hallazgos más poéticos
fue la relación entre la música y la geometría. Descubrieron que las notas musicales guardan proporciones exactas basadas en la longitud de las cuerdas, lo que los llevó a creer en la "música de las esferas".
Es interesante observar cómo este tipo de pensamiento deductivo comenzó a gestarse antes, con figuras como Tales. De hecho, el conocimiento de Tales sirvió como un cimiento fundamental sobre el cual Pitágoras construyó su visión más abstracta. Mediante la semejanza de triángulos, Pitágoras pudo ir más allá de la medición de una altura simple para entrar en el terreno de la demostración abstracta.
Además, los pitagóricos introdujeron el concepto de la "Tetraktys", un triángulo compuesto por diez puntos que simbolizaba la perfección. Para ellos, este polígono contenía la suma de las cuatro primeras dimensiones: el punto, la línea, la superficie (o área) y el volumen. Utilizando polígonos regulares, como el triángulo equilátero, demostraron que la geometría no era algo estático, sino un lenguaje dinámico. Cada ángulo y cada lado tenían un significado profundo en su cosmología.
Teorema de Pitágoras
Llegamos al corazón de su legado. Aunque existen indicios de que otras culturas conocían esta relación anteriormente, fue la escuela pitagórica la que le dio un carácter formal y universal. El teorema de Pitágoras es el puente que conecta el álgebra con la geometría, permitiendo traducir longitudes físicas en una ecuación numérica precisa. Esta proposición es válida para cualquier triángulo rectángulo, sin importar si su base mide unos centímetros o varios kilómetros.
Este enfoque de rigor lógico es lo que más tarde permitiría el surgimiento de la geometría euclidiana, donde se sistematizaron todas estas reglas mediante demostraciones que hoy estudiamos en cada clase de matemáticas.
Qué es el teorema de Pitágoras
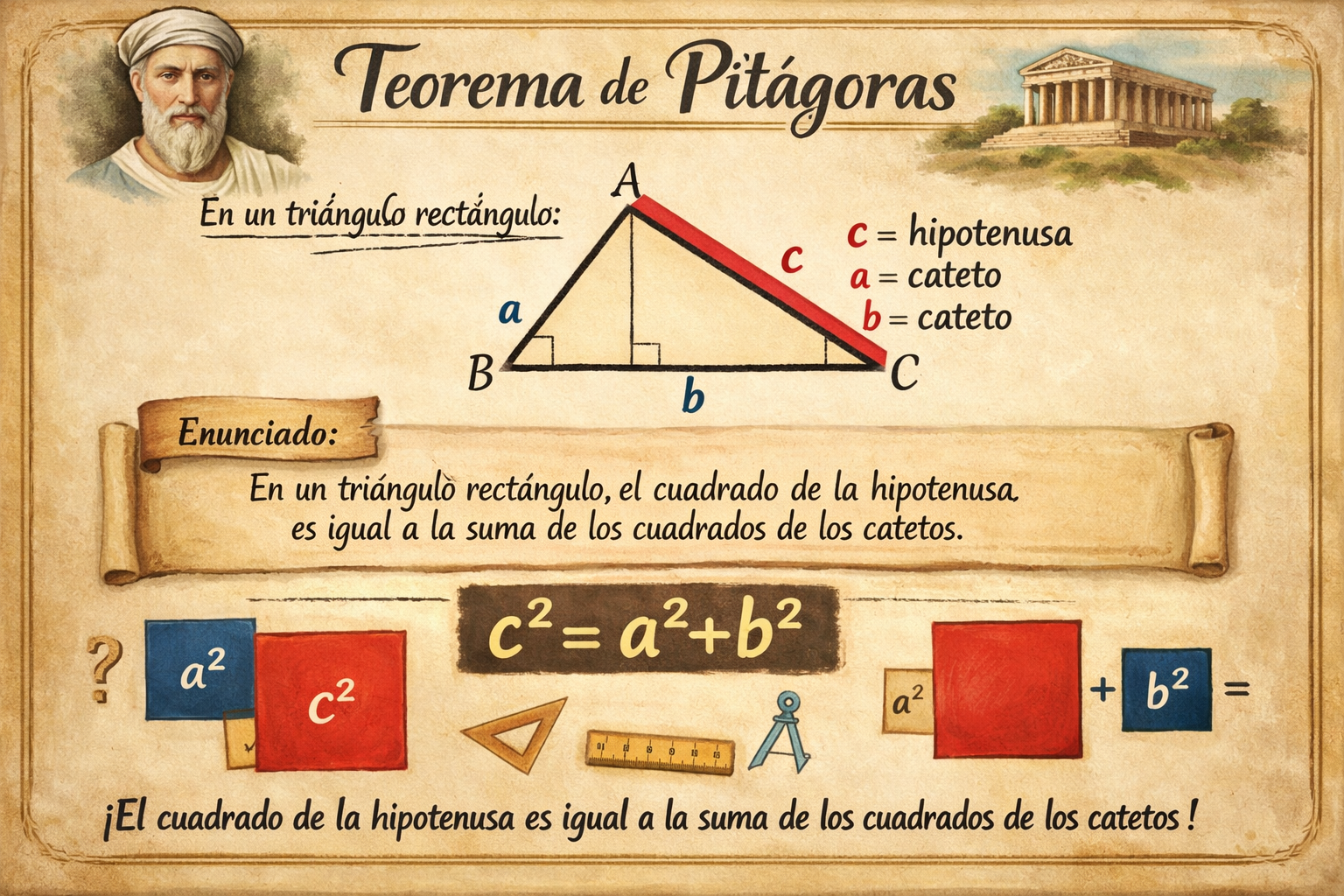
En términos sencillos, el teorema de Pitágoras establece una relación fundamental en los triángulos rectángulos (aquellos que tienen un ángulo recto de 90°). El teorema dice que el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados, llamados catetos.
La fórmula matemática se expresa así:
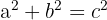
Donde 
y 
son los catetos, 
representa la hipotenusa.
Podemos visualizar esto imaginando un cuadrado construido sobre cada lado del triángulo. El área del cuadrado de la hipotenusa es exactamente igual a la suma de las áreas de los cuadrados de los catetos.
Para qué sirve el teorema de Pitágoras
La utilidad de esta fórmula es infinita y podemos encontrarla en todas partes. Se utiliza para:
Calcular la diagonal de un rectángulo
La altura necesaria de una escalera para alcanzar un muro
La distancia en una circunferencia
En arquitectura
es vital para asegurar que las bases de un edificio sean perfectamente iguales y ortogonales.
En los campos más avanzados de la ciencia
como la física teórica, estos principios básicos son necesarios.
Muchos de los posteriores avances en las matemáticas no habrían sido posibles sin comprender cómo medir el espacio utilizando triángulos. Desde hallar la diagonal de un trapecio hasta calcular la trayectoria de un proyectil, el teorema de Pitágoras es la solución universal.
Ejemplos del teorema de Pitágoras
Imagina que necesitas medir la longitud de una escalera que debe apoyarse en una pared. Si la altura de la pared es de 3 metros (un cateto) y la distancia de la base a la pared es de 4 metros (el otro cateto), ¿cómo podemos hallar la solución?
Aplicamos la ecuación:
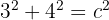
Calculamos los cuadrados:
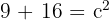
Hacemos la suma:
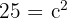
Podemos obtener el resultado con la raíz cuadrada:
Este es un ejemplo clásico de una terna pitagórica. Así, el cateto menor, el cateto mayor y la hipotenusa forman números enteros perfectos. Si te encuentras en la costa y quieres aprender a aplicar estos ejercicios de manera práctica en el diseño, buscar clases de matemáticas en Barranquilla te ayudará a dominar la geometría aplicada.
La importancia de la demostración y el área
Para un matemático de la escuela de Pitágoras, no bastaba con saber que la fórmula funcionaba; era necesario realizar una demostración rigurosa. Existen cientos de demostraciones del teorema. Una de las más visuales utiliza la semejanza de triángulos dentro de un cuadrado mayor. Al dividir un rectángulo por su diagonal, obtenemos dos triángulos rectángulos idénticos.
Al estudiar el área de estas figuras, debemos notar que el teorema también se puede extender a otras formas. Si en lugar de cuadrados, construimos triángulos equiláteros o cualquier otro polígono regular sobre los lados del triángulo recto, la relación de las áreas sigue manteniéndose: el área sobre la hipotenusa será la suma de las áreas sobre los catetos. Esto demuestra la potencia de la proposición pitagórica en toda la geometría plana.
Muchas de estas técnicas para hallar el área y trabajar con rectángulos se perfeccionaron siglos después. Por ello, conocer los descubrimientos matemáticos de otros pensadores ayuda a entender cómo la relación de Pitágoras se integró en el álgebra moderna.
El caracol pitagórico y los números irracionales
Uno de los conceptos más fascinantes es el caracol pitagórico, también conocido como la espiral de Teodoro. Se construye utilizando una serie de triángulos rectángulos donde cada hipotenusa se convierte en el cateto del siguiente triángulo. Esta figura permite medir y visualizar de forma regular las raíces cuadradas de los números naturales.
La existencia del caracol pitagórico llevó a la escuela a un descubrimiento que sacudió sus cimientos: los números irracionales. Al intentar calcular la hipotenusa de un triángulo cuyos catetos eran iguales a 1, se encontraron con 
. Este número no podía expresarse como una fracción, lo que rompió su creencia de que el mundo era solo suma de números enteros. Esta relación inesperada fue una de las demostraciones más importantes en la evolución de las matemáticas.
Para explorar cómo estos hallazgos permitieron otros avances, puedes leer sobre la evolución de las matemáticas y cómo se pasó de la geometría griega a la ingeniería de Arquímedes.
Aplicaciones avanzadas: Del trapecio a la diagonal
El uso del teorema no se limita a figuras de tres lados. Podemos aplicarlo para hallar la diagonal de cualquier polígono. Por ejemplo, en un rectángulo, la diagonal lo divide en dos triángulos donde la hipotenusa es la propia diagonal. Lo mismo ocurre en un trapecio isósceles, donde podemos hallar la altura trazando un triángulo recto desde uno de sus vértices hasta la base.
Utilizando estas herramientas, el matemático puede resolver problemas de longitud complejos en terrenos irregulares. Si te encuentras en el interior del país y deseas profundizar en cómo se calculan estas áreas, las clases de Matematicas en Bogotá son el lugar ideal para practicar con cada ecuación y cada triángulo.
Curiosidades y la mística del ángulo recto
La Pitágoras historia está llena de misterios. Se dice que el ángulo de 90 grados era sagrado porque representaba la justicia y la estabilidad. Para los pitagóricos, la igualdad 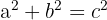no era solo aritmética; era una prueba de que el universo tenía un orden ético. Debemos recordar que ellos no separaban la ciencia de la espiritualidad.
El silencio:
Los alumnos debían pasar años en silencio antes de ser iniciados en los secretos del triángulo.
Las habas:
Pitágoras prohibía comerlas, pues creía que estaban conectadas con el mundo de los muertos.
El descubrimiento de la irracionalidad:
Se dice que cuando un discípulo reveló la existencia de (un número irracional), fue expulsado de la hermandad por romper la armonía del número entero.
El legado en el área moderna
Pitágoras no solo nos dejó un teorema; nos dejó la convicción de que el mundo es comprensible mediante la geometría. Desde la vibración de una cuerda hasta el cálculo de la diagonal de una pantalla de televisión, su visión de un universo ordenado por triángulos sigue siendo la brújula de la ciencia. El teorema de Pitágoras es mucho más que una fórmula escolar: es la prueba de que, a través de la razón y la demostración, los seres humanos podemos entender la longitud y el área del cosmos mismo. Así, cada vez que trazamos un ángulo recto y buscamos la hipotenusa, estamos caminando sobre los pasos del gran matemático de Samos.
Resumir con IA:
¿Te gustó este artículo? ¡Califícalo!
Loading...
