Tales de Mileto es recordado como el hombre que decidió que los mitos no eran suficientes para explicar el funcionamiento del mundo. En una época donde los rayos eran caprichos de Zeus y las tormentas eran la furia de Poseidón, este pensador de la antigua Grecia propuso que la naturaleza podía entenderse mediante la observación y la razón.
Su impacto en las matemáticas fue transformador porque introdujo la idea de la demostración lógica. Mientras que otras civilizaciones usaban los números para fines puramente prácticos, como contar sacos de grano o medir parcelas de tierra, Tales se preguntó por las leyes universales que regían esas formas.
¿Quién fue Tales de Mileto?
Nacido en la vibrante ciudad de Mileto, un centro de comercio y cultura en la región de Jonia, Tales vivió entre los siglos VII y VI a.C. Se le atribuye haber sido un gran viajero, visitando lugares como egipto y Babilonia, donde absorbió conocimientos astronómicos y geométricos que luego refinó con su propia lógica.
Para entender mejor su figura, podemos observar los siguientes datos clave que resumen su vida y contexto:
Personaje:
Tales de Mileto (Thales)
Época:
Aproximadamente 624 a.C. al 546 a.C.
Ciudad:
Mileto, Antigua Grecia.
Reconocimientos:
Uno de los siete sabios de Grecia.
Discípulos destacados:
Anaximandro y Anaxímenes.
Muerte:
Según crónicas, murió en el año 546 a.C. durante una Olimpiada.
Aristóteles lo describió como el iniciador de la filosofía griega por su búsqueda del arjé o principio de todas las cosas. Diógenes Laercio, por su parte, recopiló anécdotas sobre su vida, mencionando que Tales fue el primero en predecir un eclipse solar y en determinar el tamaño del sol y la luna. Era un hombre de múltiples intereses, desde la política hasta la ingeniería, siempre guiado por la curiosidad científica.
La enseñanza de las matemáticas requiere paciencia y creatividad para transformar conceptos abstractos en herramientas prácticas. Es fundamental que los docentes logren conectar la lógica con la vida cotidiana hoy.
Tales de Mileto en las matemáticas
El papel de Tales de Mileto matemáticas es el de un pionero que trajo orden al caos.
En la antigua Grecia, antes de su llegada, no existía una estructura formal para el pensamiento matemático. Él fue quien comenzó a organizar los conocimientos dispersos en un sistema coherente basado en la deducción.
Su importancia radica en los siguientes puntos fundamentales:
Introducción de la abstracción:
Pasó de medir objetos físicos a estudiar figuras ideales.
El concepto de teorema:
Estableció que una afirmación matemática debe ser probada para ser aceptada como verdad.
Relación con la naturaleza:
Utilizó las matemáticas para explicar fenómenos físicos, no solo para transacciones comerciales.
Influencia histórica:
Su enfoque permitió el surgimiento de matemáticos posteriores como Pitágoras y Euclides.
Tales de Mileto entendía que la geometría era una herramienta para descifrar el orden del universo. Según diversas opiniones de historiadores antiguos, su metodología cambió para siempre la forma en que los sabios de grecia abordaban el conocimiento, alejándose de las explicaciones místicas y acercándose a las investigaciones científicas rigurosas.
Los cursos de matemáticas en Medellín ofrecen oportunidades únicas para estudiantes que buscan reforzar sus conocimientos académicos. La ciudad cuenta con excelentes instituciones que promueven el aprendizaje lógico y el desarrollo.
Tales de Mileto y la geometría
El estudio de las formas fue la gran pasión de este filósofo. Para Tales, una linea recta o un círculo no eran simples trazos en la arena, sino conceptos con propiedades inmutables que podían ser descubiertas. Su enfoque en la Tales de Mileto geometría permitió establecer verdades que hoy estudiamos en los primeros años de formación escolar.
Entre sus descubrimientos geométricos más importantes, tradicionalmente se le atribuyen cinco teoremas que forman la base de la disciplina:
- El círculo se biseca por su propio diámetro.
- Los ángulos de la base de un triángulo isósceles son iguales entre sí.
- Al cruzarse dos líneas rectas, los ángulos opuestos por el vértice son iguales.
- Si un triángulo tiene dos ángulos y un lado igual a otro triángulo, ambos son iguales (Criterio de congruencia).
- Todo ángulo inscrito en una semicircunferencia es un ángulo recto.
Estos enunciados no solo ayudaron a resolver problemas prácticos en su época, sino que demostraron que el razonamiento humano podía alcanzar certezas universales. Tales aplicó estas reglas para calcular distancias de barcos en el mar y alturas de edificios, demostrando que la mente es capaz de medir lo que las manos no pueden alcanzar.
Contar con un profesor en linea de matemáticas permite flexibilidad horaria y acceso a explicaciones personalizadas desde casa. Esta modalidad digital facilita resolver dudas complejas de álgebra o cálculo de forma.
¿Qué es el teorema de Tales de Mileto?
El teorema de Tales de Mileto es la regla de oro de la proporcionalidad en geometría. En términos muy sencillos, nos explica qué sucede cuando cortamos un conjunto de líneas paralelas con otras dos líneas transversales. El resultado es una armonía perfecta de proporciones entre los segmentos creados.
Este teorema es la base de la semejanza de triángulos. Nos dice que si dos figuras tienen la misma forma pero diferente tamaño, sus lados correspondientes siempre mantendrán una relación numérica constante. Es como el zoom de una cámara moderna: la imagen cambia de tamaño, pero las proporciones de los objetos dentro de ella se mantienen idénticas.
Hubo un místico matemático Griego cuya influencia perdura hasta hoy. Su famoso teorema de Pitágoras sobre los triángulos rectángulos estableció una relación fundamental entre la geometría y el álgebra antigua.
En qué consiste el teorema de Tales
Para comprender paso a paso en qué consiste el teorema de tales, imaginemos dos rectas cualesquiera, que llamaremos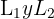 
. Si estas rectas son interceptadas por tres o más líneas paralelas entre sí, los segmentos que resultan en la primera recta serán proporcionales a los segmentos correspondientes en la segunda recta.
Podemos representar esta relación mediante una fórmula sencilla. Si los puntos de corte en la primera recta son 
, y en la segunda son 
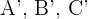, entonces se cumple que:
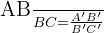
Esta igualdad nos permite encontrar una medida desconocida si conocemos las otras tres. Es una aplicación directa de la proporcionalidad que facilita enormemente el trabajo en arquitectura y diseño. Lo que Tales descubrió fue que la distancia física no importa tanto como la relación matemática entre los elementos.
El proceso para aplicar el teorema suele seguir este orden:
- Identificar las líneas que son paralelas entre sí.
- Localizar las rectas transversales que las cortan.
- Establecer la relación de proporcionalidad entre los segmentos conocidos y el desconocido.
- Resolver la ecuación para hallar el valor faltante.
Las clases de matemáticas en Cali son ideales para quienes desean superar dificultades escolares en un ambiente dinámico. Los tutores locales utilizan métodos innovadores para enseñar conceptos de geometría de manera.
Para qué sirve el teorema de Tales
Muchos estudiantes se preguntan para que sirve el teorema de tales en el mundo real. La respuesta es fascinante, ya que sus aplicaciones han moldeado la historia del progreso humano desde la antigua Grecia hasta nuestros días.
Aquí presentamos algunas de las utilidades más comunes:
Medición de alturas inaccesibles
La historia del teorema de tales cuenta que el filósofo midió la altura de las pirámides de egipto observando su sombra. Al colocar un bastón vertical y comparar su sombra con la de la pirámide, pudo establecer una proporción exacta sin tener que trepar ni un solo escalón.
Los Elementos de Euclides representan uno de los libros más influyentes de la historia humana. En esta obra, se sistematizaron los conocimientos geométricos mediante definiciones, postulados y demostraciones lógicas rigurosas.
Cálculo de distancias geográficas
En la navegación y la topografía, este teorema permite calcular el ancho de un río o la distancia de un barco a la costa sin necesidad de cruzar el agua. Basta con crear un sistema de triángulos semejantes en la orilla.
La investigación matemática es un proceso constante de descubrimiento que impulsa la tecnología moderna. Científicos de todo el mundo trabajan diariamente para encontrar patrones numéricos que resuelvan problemas complejos actuales.
Diseño a escala y maquetación
Desde los planos de una casa hasta el diseño de piezas mecánicas pequeñas, el teorema de tales asegura que las proporciones se mantengan correctas al cambiar el tamaño de un objeto. Esto es vital en la ingeniería civil y la arquitectura moderna.
Perspectiva en el arte
Los artistas utilizan los principios de Tales para crear profundidad en sus cuadros. Al entender cómo las lineas convergen y cómo los objetos se reducen proporcionalmente con la distancia, pueden engañar al ojo humano para percibir tres dimensiones sobre un lienzo plano.
Inscribirse en cursos de matemáticas en Bogotá brinda acceso a una formación académica de alto nivel. La capital colombiana dispone de centros especializados donde el razonamiento lógico es siempre la prioridad.
Astrofísica y óptica
El estudio de cómo se proyectan las sombras durante los eclipses o cómo las lentes de un telescopio enfocan la luz se basa en los mismos principios de proporcionalidad que Tales formuló hace más de dos mil quinientos años.
Cada estudiante que logra resolver un problema difícil aporta su propio granito de arena a las matemáticas. El esfuerzo individual construye el conocimiento colectivo necesario para entender mejor nuestro universo.
Como hemos visto, el legado de Tales de Mileto es inmenso. No solo nos dejó fórmulas útiles, sino que nos enseñó a confiar en nuestra capacidad de razonar. Su vida dedicada a la filosofía y a la ciencia nos recuerda que, a menudo, los problemas más grandes pueden resolverse con una observación inteligente y un simple bastón bajo el sol. Según Aristoteles, su trabajo fue el primer paso real hacia la comprensión lógica de nuestro lugar en el universo.
Las investigaciones científicas dependen en gran medida de modelos matemáticos precisos para validar hipótesis. Sin los números, sería imposible medir la realidad o realizar predicciones exactas sobre el clima mundial.
Resumir con IA:
¿Te gustó este artículo? ¡Califícalo!
Loading...
