En el fascinante mundo de las matemáticas, nos encontramos frecuentemente con diferentes tipos de relaciones entre variables. Una de las más importantes y fundamentales es la función afín. Pero, ¿qué es una función afín? Una función afín es aquella que combina una parte lineal con un término constante, creando una relación matemática que aparece en numerosas situaciones cotidianas.
En este artículo exploraremos en profundidad el concepto de qué es una función afín para tus clases de matemáticas, desde sus características básicas hasta sus aplicaciones más prácticas. Descubriremos cómo identificarlas, representarlas gráficamente y utilizarlas para resolver problemas del mundo real. A través de ejemplos claros y explicaciones detalladas, aprenderemos a distinguir entre funciones afines y lineales, comprenderemos sus propiedades fundamentales y desarrollaremos las habilidades necesarias para trabajar con ellas de manera efectiva en diversos contextos matemáticos y prácticos.

¿Qué es una función?
Antes de adentrarnos en las funciones afines, es fundamental comprender qué es una función en matemáticas. Este es un viniculo especial entre dos conjuntos de números, donde a cada elemento del primer conjunto (llamado dominio) le corresponde exactamente un elemento del segundo conjunto (llamado codominio o rango). Podemos pensarla como una máquina que toma un número como entrada y produce otro número como salida, siguiendo siempre la misma regla.
Por ejemplo, cuando calculamos el área de un cuadrado, estamos usando una función: para cada longitud del lado (entrada), obtenemos un único valor de área (salida). Si el lado mide 2 unidades, el área será siempre 4 unidades cuadradas. Esta relación predecible y consistente es lo que hace que sea una función.
Las funciones son herramientas poderosas en matemáticas y estadística porque nos permiten modelar relaciones entre cantidades que cambian. Pueden representar desde situaciones cotidianas, como el costo de una llamada telefónica según su duración, hasta fenómenos naturales complejos, como el crecimiento de una población o la caída de un objeto.
Definición de función afín
Imagina que tienes una franja en un plano. Esa franja puede representar muchas cosas en la vida real: la velocidad de un coche a medida que pasa el tiempo, el crecimiento de una planta, o incluso el costo de comprar manzanas en un mercado.
Una función afín es simplemente una manera matemática de describirla.
Cuya fórmula sigue el patrón y = mx + n, donde m y n son números distintos de cero
Donde:
f(x): Es el valor que obtenemos en la recta para un determinado valor de x.
x: Es la variable independiente, como el tiempo o la cantidad de manzanas.
m: Es la pendiente de la recta, que nos indica qué tan inclinada está.
b: Es la ordenada al origen, que es el punto donde la recta corta al eje y.
Si te preguntas ¿cómo saber si una función es lineal o afín?, te contamos que diferenciar entre funciones lineales y afines es fundamental en el estudio de las matemáticas, ya que cada una describe un tipo particular de víniculo entre variables y tiene aplicaciones específicas. Aborda estas nociones y preguntas durante las clases de estadistica con tu profesor particular.
¿Cuál es la diferencia entre función afin y lineal?
Función lineal:
- Forma: f(x) = mx
- Características:
- Siempre pasa por el origen (0,0).
- La relación entre las variables es de proporcionalidad directa.
- La pendiente (m) indica la tasa de cambio constante.
- Ejemplo: El costo de comprar manzanas a un precio fijo por unidad.
Función afín:
- Forma: f(x) = mx + b
- Función afín características:
- No necesariamente pasa por el origen.
- El víniculo entre las variables es lineal, pero puede tener un desplazamiento vertical.
- La pendiente (m) indica la tasa de cambio constante, y la ordenada al origen (b) indica el valor inicial o el punto de corte con el y.
- Representación gráfica:
- Siempre es una línea derecha: Esta es la característica más distintiva de una función afín.
- La pendiente (m) determina la inclinación
- La ordenada al origen (b) determina el punto de corte con el y:
- El punto (0, b) siempre pertenece a la vista de la función.
- Tasa de cambio constante:
- La pendiente (m) representa la tasa de cambio constante de la función. Esto significa que por cada unidad que aumenta x, y aumenta (o disminuye) en m unidades.
- Dominio y rango:
- Dominio: El conjunto de todos los números reales.
- Rango: También es el conjunto de todos los números reales, a menos que la función esté restringida a un cierto intervalo.
- Intersección con los ejes:
- y: Corta al y en el punto (0, b).
- x: Corta al x en el punto (-b/m, 0), si m ≠ 0. Si m = 0, es horizontal y no corta al x a menos que b = 0.
- Aplicaciones:
- Modela situaciones reales donde existe un víniculo lineal entre dos variables.
- Se utiliza en física, economía, ingeniería, y muchas otras áreas.
- Ejemplo: El costo de alquilar una bicicleta, donde hay un costo fijo inicial más un costo por hora. Aprende a aplicarlo en casos reales.
¿Por qué es importante diferenciarlas?
- Interpretación de datos: Cada tipo de función representa un fenómeno diferente. Por ejemplo, una función lineal modela situaciones donde una cantidad aumenta o disminuye proporcionalmente a otra, mientras que una función afín puede modelar situaciones con un valor inicial fijo.
- Resolución de problemas: Al identificar correctamente el tipo de función, se pueden utilizar las herramientas matemáticas adecuadas para solucionar problemas. Una buena opción para entenderlo es tomar cursos de matematicas basicas.
- Graficación: La representación de una función lineal siempre pasa por el origen, mientras que la representación de una función afín puede estar desplazada verticalmente.
- Aplicaciones: Ambas funciones tienen aplicaciones en diversas áreas, como física, economía, ingeniería, etc. Comprender la diferencia es esencial para elegir el modelo matemático correcto para cada situación.
Aunque las funciones lineales y afines son similares, la presencia de la constante "b" en la función afín marca una diferencia fundamental. Esta constante permite modelar una mayor variedad de situaciones reales y hace que la función afín sea más versátil que la función lineal.
Para ilustrar mejor, imagina que estás graficando el crecimiento de una planta. Si la planta crece a una tasa constante y comienza desde cero centímetros, una función lineal sería el modelo adecuado. Sin embargo, si la planta ya tenía una cierta altura al inicio de la medición, una función afín sería más apropiada para representar su crecimiento. Otro tema que te puede interesar descubrir es la división euclídea.

Hacer la representación gráfica de una función afín
La representación de una función afín es siempre recta. Esto es una de las características más distintivas de estas funciones.
Recordemos que la ecuación general de una función afín es:
f(x) = mx + b
m: indica qué tan inclinada está.
b: es la ordenada al origen, que es el punto donde corta al eje y.
Estos dos valores, m y b, determinan completamente la posición y la inclinación en el plano cartesiano.
Elementos clave:
- Pendiente (m):
- Si m > 0, es creciente (sube de izquierda a derecha).
- Si m < 0, es decreciente (baja de izquierda a derecha).
- Si m = 0, es horizontal.
- Ordenada al origen (b):
- Indica el punto donde corta al y. Es decir, el punto (0, b).
La imagen representa el gráfico de dos funciones afines diferentes:
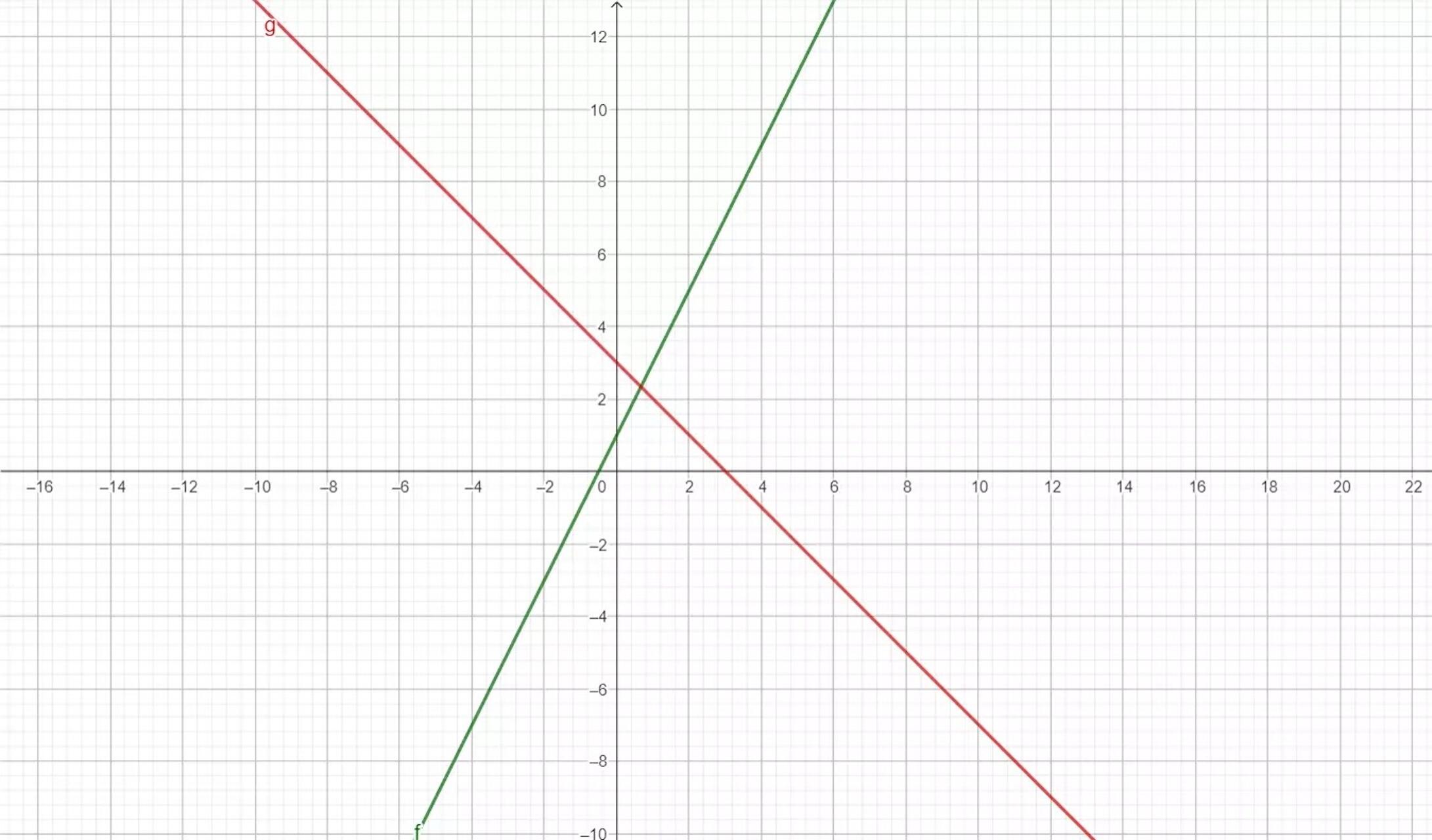
Cada una de las líneas en el gráfico corresponde a una función afín distinta. Una función afín, como ya sabes, es una función matemática cuya representación es siempre una línea recta.
- f(x) = 2x + 1:
- Pendiente (m): 2 (positiva, por lo que es creciente).
- Ordenada al origen (b): 1 (corta al eje y en el punto (0, 1)).
- Interpretación: Esta función representa una línea que sube de izquierda a derecha y cruza el eje y en el punto (0, 1).
- g(x) = -x + 3:
- Pendiente (m): -1 (negativa, por lo que es decreciente).
- Ordenada al origen (b): 3 (corta al y en el punto (0, 3)).
- Interpretación: (0, 3).
¡Descubre también qué es la geometría!.

La función afín gráfica es una herramienta visual muy útil para entender su comportamiento y sus propiedades. Al conocer la pendiente y la ordenada al origen, puedes construir la gráfica de cualquier función afín de manera sencilla.
¿Cómo determinar una función afín?
En una función f es fácil si conocemos los valores de «a» y «b». En nuestro ejemplo f(x) = 2x – 3.
Decimos que f(2) = 1, que f(– 2) = – 7 y que f(1) = – 1.
Para calcular nuestra función, podemos emplear dos métodos: el cálculo y la lectura sobre los ejes de coordenadas. Si apenas se está empezando, puedes buscar una clase de matematicas para niños.

Hacer el cálculo a partir de la representación
Es el método menos complicado, pero a partir de la segunda clase, como verás, no siempre vendrá en los ejercicios.
Para la interactiva f(x) = 2x – 3, bastará con ver qué puntos de las rectas cortan los x y. En nuestro caso, encontramos los puntos A (0; – 3), B (2; 1) y C (3;3), de donde deducimos que la recta d1 presenta tipo y =2x – 3.
Determinar una función mediante cálculos
Si no contamos con la descripción gráfica o el profesor nos pide que razonemos cuál es la expresión, ¿Cómo lo podemos hacer?
Pues aquí te dejamos una fórmula mágica:
Cuando f es una función afín no lineal, los valores de «x» que cumplen f(x) no son proporcionales; sin embargo, sí lo son entre los valores de «x».
Para calcular el coeficiente de dirección con dos números x1 y x2 y su presentación f: a =Tenemos que x1 = 0 y x2 = 0, con f(x1) = – 3y y f(x2) = 1.
Al reemplazar las incógnitas, obtenemos a = (– 3, – 1) / (0, – 2) = – 4 / – 2, donde a = 2.
¡Descubre qué es el álgebra!
Estudiar el signo de una función afín
Ahora que tenemos la pendiente y su descripción, ¿Cómo estudiamos el signo de f?
Cualquier persona que haya cursado estudios superiores de estadística, sin tener que ser «matemática» pura, habrá estudiado la noción del signo.
Si «a» es positivo, la función f aumenta y si no, esta terminara siendo negativa.
Si x1 < x2, entonces ax1 < ax2 y ax1 + b < ax2 + b y f(x1) < f(x2). En este caso, – 2 es inferior a 0 y – 7 es inferior a – 3.
Por lo tanto, nuestra función f(x) = 2x – 3 es creciente. Los valores de f(x) comenzarán así de negativo a positivo cruzando el punto 0 en la ordenada – 3.
La ecuación ax + b = 0 (siendo a ≠ 0) tiene una solución única que es x = ((– b) / a). Cada recta de la ecuación y = ax + b corta el eje de abscisas en el punto de matrices ((– b/a; 0).
Como b = – 3 y a = 2, deducimos que el signo de f es positivo en el punto de coordenada (2/3; 0).
Para estudiar la variación de f(x), tendrás que conocer la derivación matemática.
Ten en cuenta que f es derivable en todos los ℝ y que para todo x∈ℝ, f ‘(x) = 2x – 3 = 2. Por lo que f ‘ (x) es positiva.
Los signos de f serán: negativos de – ∞ al punto 2/3, y positivo desde el punto 2/3 hacia +∞.
Para no perderte con tantos conceptos, puedes apuntarte a clases de matematicas online. Y si vives en la capital, no dudes en buscar clases particulares en Bogotá.
Aprende a dominar el tema
Resulta que la matemática y cada descripción que esta tiene, son útiles en la vida cotidiana, a veces sin importar el camino que tomes. Que tal que en el proceso de graficar ecuaciones lineales o ecuaciones a fin, te decidas por una carrera que tenga que ver con esto.
Toma cursos virtuales
La mayoría de los cursos de matematicas bogota virtuales son creados por instituciones que desean ver un mejor desempeño de sus estudiantes, a la hora de graficar ecuaciones, o de hacer la descripción de un ejercicio. En estos cursos podrás aprender las diferentes técnicas y métodos elementales que existen actualmente para poder solucionar sistemas de funciones lineales y a fin.
Los videos
Subir un video a la red, es una forma simple de compartir conocimientos y de hacer ver a el estudiante que realmente cada función lineal o cada función a fin es importante en la vida cotidiana desde la múltiplicación de números reales hasta ecuaciones complejas. Aunque en un video no encontramos ejercicios interactivos, podemos ver función afin ejemplos como este:
Dada la siguiente situación, resuelva las preguntas.
Un tanque contiene 9.000 litros de agua. Para vaciarlo, se recurre a una bomba que tiene capacidad de extraer 1000 litros de agua por minuto.
Entre las preguntas podemos ver que la principal sería. ¿Cuánto tiempo tardará la bomba en vaciar el tanque? Lo primero que debemos hacer para representar el ejercicio es una tabla.
| Tiempo que ha trascurrido | Cantidad de agua dentro del tanque. |
|---|---|
| 2 | 9300 |
| 4 | 9100 |
| 6 | 8900 |
| 8 | 8700 |
Para crear la tabla debemos encontrar los valores según los números que elegimos:
La fórmula es 9.000 litros de agua que tiene el tanque - 1000 (litros extraídos por minuto) * x (tiempo que queremos encontrar).
¡Hagámoslo!
9.000 - ( 1000* 2 = 2000) 2000 = 7.000.
9.000 - (1000*4 = 4000 ) 4000 = 5000.
9.000- ( 1000*6= 6000 ) 6000 = 3.000.
9.000- ( 1000 * 8= 8000) 8000 = 1.000.
Ahora veamos cual es la dependiente y la variable de la situación dada.
Dependiente: (Y) cantidad de agua en el tanque.
Independiente: (X) cantidad de tiempo transcurrido.
¿Cuál sería la fórmula?
9.000 - 1000x = y
y = 9.000 = 1000x
Ahora vamos a revisar la primer pregunta. Por simple razonamiento podemos deducir que cuando el tanque quede vacío, la cantidad de agua es de 0. Así que planteemos lo siguiente:
y = 9.500-1000x
Cambiamos y por 0 ya que deducimos que al vaciar el tanque la cantidad de litros es 0.
0 = 9.500 - 1000x
Finalmente solo nos queda un valor por la que sería la (x) del tiempo que tarda en vaciar el tanque. Para ello debemos despejar al (x) donde el 9.500 pasa a restar el menos 100 pasa a dividir.
0 - 9.000= -1000x
- 9.000 : (-1000) = x
9 = x
El tanque de 9.000L con una bomba que extraiga 1000L de agua, tardara 9 minutos en quedar vacío.
Ahora por último, nos queda graficar la evolución del ejercicio que tuvimos en escena.

Aunque ciertamente para entender mejor, la mejor opción es subir un video, en la gráfica podemos evidenciar que la recta no pasa por por el eje 0, y representa el volumen del tanque a medida que la bomba de agua va cumpliendo con su función.
Las funciones afines son herramientas matemáticas fundamentales que nos permiten modelar numerosas situaciones del mundo real. Su comprensión es esencial para el estudio de matemáticas más avanzadas y su aplicación en diversos campos profesionales.
El dominio de estos conceptos abre puertas para entender relaciones más complejas y desarrollar habilidades de pensamiento matemático más sofisticadas. Con práctica y dedicación, cualquier estudiante puede llegar a dominar este importante concepto matemático.
Resumir con IA:

















Buenas tardes. A mí hija le enviaron una tarea que dice escribe el uso de la función afín. La verdad aún no logro comprender muy bien querés la función afín mucho menos cuál es su uso. Si me pudiesen ayudar les agradecería.
una pregunta cual es la importancia de una función afin para las carreras de fisica matemática ingenieria y arquitectura
genial muy facil