Las teorías matemáticas nos rodean en todos lados constantemente; es un poco como si viviéramos continuamente en el eje de la matriz de Neo (de la película Matrix).
Cuando miras la distribución o el plano de tu casa, la disposición de cada recta en las calles de tu barrio, cuando arrancas tu coche, cuando trabajas las celdas de Excel, cuando buscas coordenadas en un plano, las mates y la geometría están ahí, por eso decimos que las mates nos pueden ayudar a entender el mundo que nos rodea y verlo de diferentes ángulos.
el autor Ian Stewart, un científico británico de renombre, publicó una obra titulada Las 17 ecuaciones que cambiaron el mundo (Ed. Robert Laffont en 2013.)
Cada ecuación es interesante y tenemos razones de peso para estudiar esta disciplina, ahora si quieres saber qué impactos ha tenido cada ecuación, a continuación te presentamos algunas de estas ecuaciones matemáticas difíciles pero totalmente revolucionarias.

1. El teorema de Pitágoras
Al igual que la circunferencia, el vector o los ángulos, este termino es seguramente uno de los más conocidos, pues lo solíamos estudiar desde que tomábamos clases de matematicas para niños en el colegio.
Sin embargo; vamos a refrescarte la memoria: en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Esta fórmula es esencial para entender mejor las figuras y graficas geométricas; de hecho, esta fórmula ha cambiado nuestra forma de ver la geometría.
A partir de entonces, gracias a Pitágoras y a su famosa ecuación, es fácil calcular longitudes y ángulos y demostrar que un triángulo es rectángulo.

2. El teorema de Tales
Este es un segundo pilar de los cursos de matematicas en bogota.
Este teorema no es de Tales, sino de Euclides, pero se le atribuyó a Tales por la leyenda de la medida de la pirámide.
Definición: "Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado".
Del establecimiento de la existencia de una relación de semejanza entre las figuras de ambos triángulos y por ende de sus ángulos, se deduce la necesaria proporcionalidad entre sus lados. Este corolario es la base de la geométrica descriptiva.
Pero ¿Cómo aporta una solución real a problemas concretos?
En geometría, el test de Tales, tal como su corolario, también puede utilizarse para mostrar y establecer condiciones de alineamiento o de paralelismo entre figuras geométricas, o en un plano.
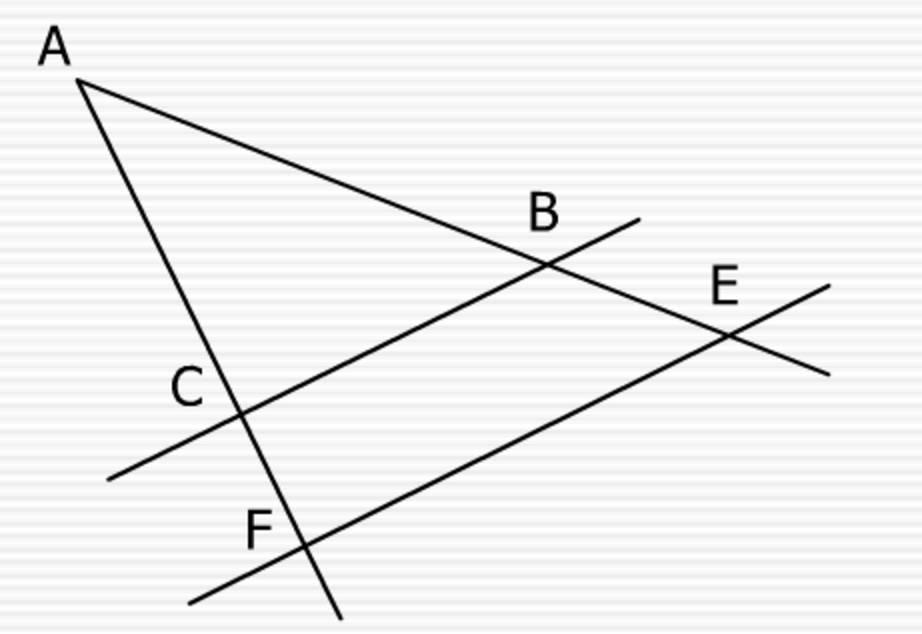
La leyenda cuenta que a petición del rey Amasis, Tales fue a Egipto para calcular la altura de las pirámides, y en concreto la de Keops.
Colocando un bastón en vertical a mediodía, le dijo al rey: "La relación con respecto a mi sombra es la misma que la de la pirámide con respecto a la suya".
Así, en otros términos, si la longitud del bastón de este modo como su sombra son sabidas, es posible y aplicando la misma distribución, determinar la altura de las pirámides, tras medir la sombra.
3. Los logaritmos
El log, popularizado por John Napier en 1610, agrupa funciones inversas, funciones opuestas y funciones exponenciales. El logaritmo es el exponente al que hace falta elevar su base para obtener dicho número.
Por ejemplo; en lo que respecta a la base 10, el logaritmo (log) es: Log (1) = 0, log (10) = 1, log (100) = 2.
Los logaritmos son frecuentes en las fórmulas utilizadas en ciencias. Estos miden la complejidad de fractales y aparecen en fórmulas que permiten contar los números primarios.
Hasta la llegada del ordenador, el cálculo con log era la forma más habitual de multiplicar números grandes. Los logaritmos permitieron calcular de forma muy rápida, pero sobre todo hacer grandes avances matemáticos, fisicos e incluso avances en el área de la ingeniería.
Hay tres tipos de logaritmo:
- Neperiano: es la base fundamental en el análisis matemático (por lo cual lo podemos encontrar en clases de estadistica)
- Decimal: se utiliza en cálculos matemáticos.
- Binario: se utiliza en la teoría informática y para cálculos aplicados.
4. La ley de la gravedad
¿Quién no ha oído nunca hablar de la ley de la gravedad de Isaac Newton? Ya sabes, la historia de la manzana que le cayó en la cabeza al erudito mientras miraba el circulo que hace la Luna en el cielo. Eso pasó en 1687.
Tras la caída de la manzana, miró de nuevo las figuras de la Luna y las estrellas y pensó: ¿por qué la Luna no se cae? La respuesta es evidente: la «retiene» una fuerza gravitatoria.
De esta forma fue como nació la célebre fórmula de la ley de la gravedad de Newton:
«Los astros se atraen de forma proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa».
Newton
Doscientos años luego, Einstein remplazo la serie de la gravitación por su teórica de la relatividad, y aun te preguntas, ¿para qué sirven las mates en nuestro día a día?
5. La teoría de la relatividad
Tanto los matemáticos como los físicos, todos conocen la famosa fórmula E = mc² de Albert Einstein.
Esta fórmula que ilustra las teorías de la relatividad, alteró todos los códigos de la matemática hasta entonces. Actualmente, sigue siendo de las formulas cruciales, ya que suele mostrar que la materia puede convertirse en energía y viceversa.
La relatividad especial, o restringida, aporta la idea de que la velocidad de la luz es una constante universal que no cambia y que el paso del tiempo no es el mismo para las personas que se desplazan a velocidades diferentes.
La relatividad general de Einstein describe la gravedad donde existe un espacio-tiempo curvado y plegado, lo que supuso un cambio fundamental tras la ley de la gravedad de Newton.
Actualmente, todavía es esencial la serie de la relatividad de Einstein para mostrar y entender el origen, la estructura y el destino de nuestro mundo. Podríamos decir que esta es de esos Enigmas Matemáticos Difíciles de Resolver.
6. La teoría del caos
Lo que es interesante de la serie del caos es que, aplicando sus formulas, nos suele mostrar que no se puede predecir con determinación lo que va a ocurrir.
Esta teoría prueba que no existe ningún proceso o distribución que se pueda pronosticar.
La teoría de Robert May es muy reciente, ya que data de 1975 y se enfoca en mostrar un proceso en constante evolución a través del tiempo.
En su fórmula, May quiso explicar que un comportamiento caótico (como la meteorología que conoce muchos cambios climáticos regularmente, incluso ínfimos) puede conducir a otro sistema completamente diferente unos días después.
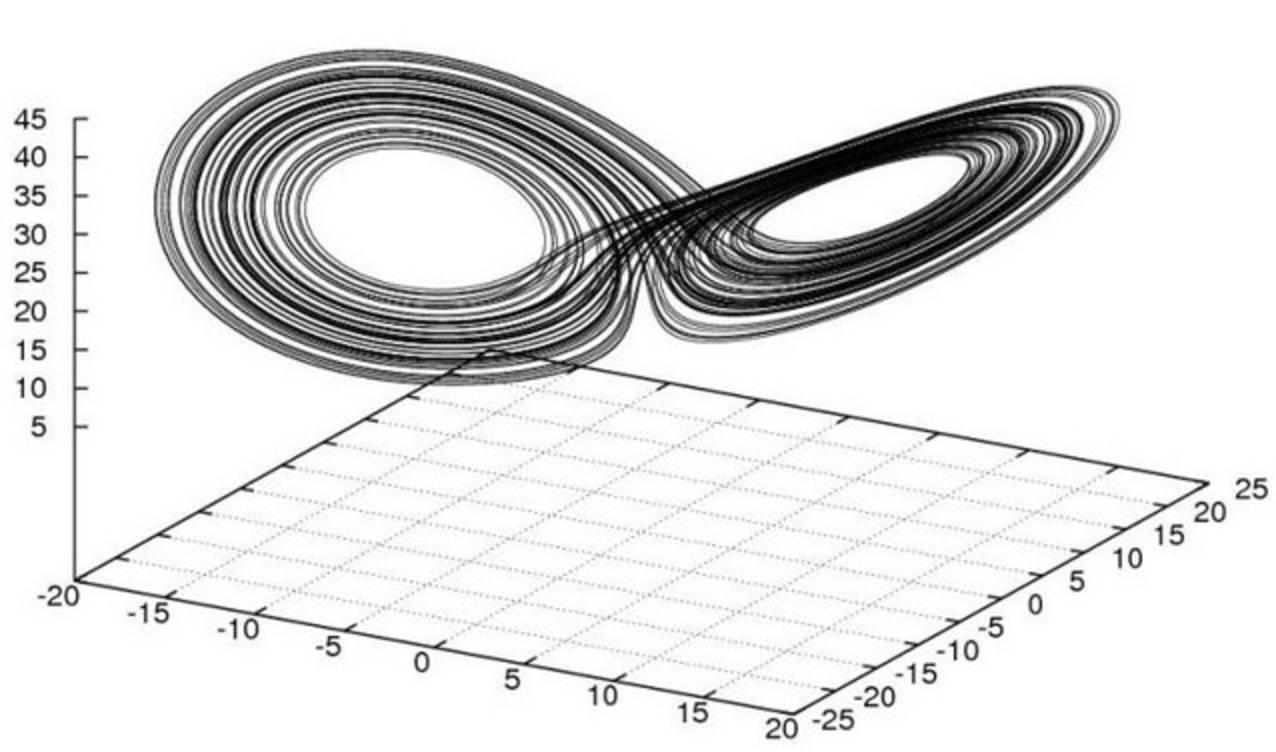
El concepto más conocido es el del «efecto mariposa» que afirma que «el aleteo de las alas de una mariposa tiene una alta probabilidad de provocar un tornado al otro lado del mundo».
En otras palabras, las cosas muy insignificantes tienen una alta probabilidad de tener un impacto insospechado en nuestro entorno inmediato y menos inmediato.
La multiplicidad de los factores hace que todo acontecimiento sea imprevisible. Esto lo podemos aprender mejor con un profesor de matematicas en linea.
7. El cálculo infinitesimal
A medio camino entre el álgebra y la grafica geométrica, el cálculo infinitesimal es una rama de las mates. El dato infinitesimal se centra en las integrales, las series o sucesiones infinitas, las operaciones, tratando sus derivadas y sus límites.
Para resumirlo en una sola idea, hablaríamos de estudio de variaciones. Encontramos un elevado número de formulas aplicables en la mecánica, la física o la economía.
En efecto, el estudio de variaciones permite estudiar la evolución de una empresa teniendo en cuenta muchos datos diversos para predecir o dar una idea de su salud financiera en años futuros.

8. La identidad de Euler
La identidad de Euler está considerada como la mejor de las formulas o ecuaciones, ya que pone en escena una combinación improbable de cinco constantes.
¿Por qué es tan admirada esta ecuación? Porque utiliza tres de las operaciones fundamentales de la aritmética: la suma, la multiplicación y el exponente.
Las cinco constantes representadas con el «0», que es el elemento neutro de la suma; el «1», que es el elemento neutro de la multiplicación; el número pi; la «e», que es la base de los logaritmos (y que aparece a menudo en análisis y cálculos diferenciales) y la «i», que es la unidad imaginaria, a partir del cual se construye el conjunto de los números complejos que encontramos en las operaciones de tres incógnitas.
Esta función ha abierto el camino al desarrollo de la topología, un área de la matemática moderna.
Y además de ayudarte a entender todas estas formulas increíbles, las mates te pueden servir para aumentar tu capacidad de seducción en el plano amoroso.
9. La transformada de Fourier
La transformada de Fourier divide el tiempo en varias frecuencias y ondas simples, como un prisma desglosa la luz en varios colores.
Un ejemplo podría ser un campo magnético o un campo acústico, que se definen como una señal; la transformada de Fourier es su espectro: desestructura el campo acústico o magnético.
Esta teoría transformó nuestro mundo, ya que de repente era posible entender la circunferencia o la estructura de las ondas más complejas como la del habla humana.
Actualmente, encontramos esta serie, que data del 1822, en los procesamientos modernos de señal y de análisis, al igual que del procesamiento de datos.
10. Las ecuaciones de Maxwell
Las ecuaciones de Maxwell describen cómo interactúan las cargas eléctricas y del mismo modo las corrientes eléctricas y los campos magnéticos.
Explican el comportamiento de la relación entre la electricidad y el magnetismo y son leyes esenciales y fundamentales de la física de hoy en día.
Hay cuatro formas de ecuaciones de Maxwell:
- Ecuación de Maxwell-Faraday
- Ecuación de Maxwell-Ampère
- Ecuación de Maxwell-Gauss
- Ecuación de Maxwell-Thomson
¿Demasiados datos de golpe? No te preocupes, un curso de matematicas basicas desde cero te ayudará a tomártelo con calma.
11. El segundo principio de la termodinámica
El segundo principio de la termodinámica (igualmente conocido como el principio de Carnot, que lo enuncia en 1824) prueba de manera irrefutable que los fenómenos físicos son irreversibles, principalmente cuando hay cambios térmicos.
Este principio también fue cambiado y reformulado en varias ocasiones y fue Ludwig Boltzmann en 1873 con Max Planck quienes lo popularizarán a gran escala.
Mientras que el primer principio de la termodinámica establece una equivalencia de diferentes formas de energía, como el calor y el trabajo (principio de conservación), el segundo principio introdujo otro sistema llamado entropía.
Es un principio de evolución, ya que determina en qué dirección las posibles transformaciones energéticas son factibles.
Por eso también, se pueden dar ciertas transformaciones químicas, mientras que otras nunca lo se darán.
Por ejemplo, si pones un cubito de hielo en una taza de café caliente, verás que el cubito de hielo se derrite pero nunca verás que el café se congela. ¿Te apasiona el póker? Descubre cómo las mates te pueden ayudar a dominarlo.
12. La ecuación de Schrödinger
Si tuviéramos que ilustrar qué son las mates y la mecánica cuántica, el patrón de Schrödinger sería el ejemplo perfecto.
Al igual que la serie de la relatividad general de Einstein pudo explicar el mundo a gran escala, esta función también arroja luz sobre el comportamiento de los átomos y las partículas subatómicas.
La operación de Schrödinger explica la evolución en el tiempo de una partícula. Describe los estados de esta partícula a partir de los cuales se puede describir todos los estados compuestos de partículas.
Esta función plantea una auténtica cuestión filosófica, a saber: ¿la materia se compone de presencias de los estados posibles (gas, sólido, líquido)? ¿No hay nada más?
La aplicación de esta ecuación se encuentra en la tecnología moderna, como la energía nuclear, los ordenadores con semiconductores y los láseres. Como puedes ver es tan interesante como para aprenderle mejor en unos cursos de matematicas en medellin.
13. Las ecuaciones de Navier Stokes
Encontramos estas propiedades en mecánica de fluidos. Describen el movimiento de fluidos newtonianos (gas y ciertos líquidos) que tienen la particularidad de tener derivadas parciales no lineares.
Aunque la coherencia de cada ecuación (no linear) no esté demostrada, a menudo permiten una modelización de fenómenos relativamente cercana de la realidad percibida.
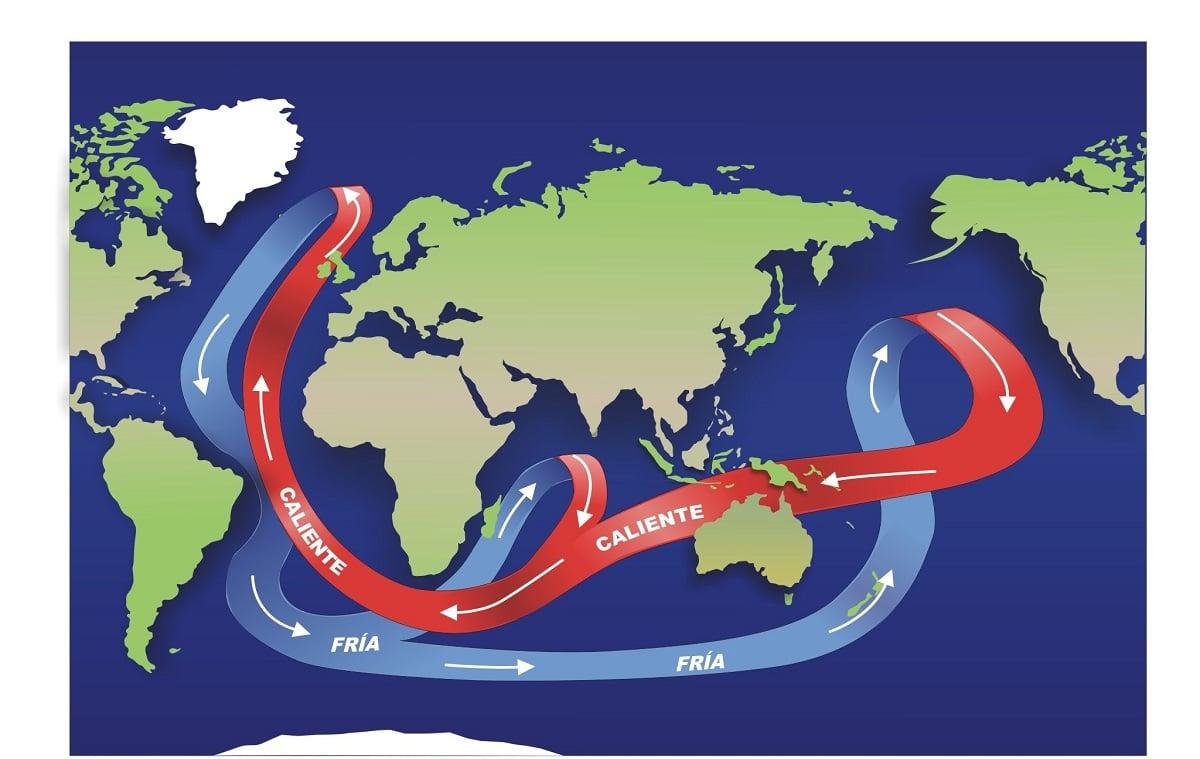
Estas ecuaciones son útiles en ámbitos como las corrientes oceánicas, la meteorología con los movimientos de masa de aire en circulo u horizontal, el comportamiento de las construcciones (edificios, puentes) ante el impacto del viento o el comportamiento de los objetos lanzados a gran velocidad, como un tren o un avión frente al viento.
14. La teoría de la información de Shannon
Esta serie haya sus fundamentos en el artículo A Mathematical Theory of Communication publicado en 1948 por Claude Shannon y será completada por Warren Webber después. Esta considera la información como una variable cuantificable, aunque no se pueda observar.
Una vulgarización de esta serie consistiría en decir que se centra en cuantificar el contenido medio de datos contenido en un mensaje o en un conjunto de mensajes.
Aunque este concepto teórico de los datos no se limita inicialmente más que al análisis de medios a poner en marcha para transmitir unos datos lo más eficaces posibles, muy pronto fue objeto de una reapropiación aritmética, en especial a través de los trabajos del estadista Ronald Aylmer Fisher.
Fisher destaca el hecho de que una información es igual al valor medio del cuadrado de la derivada parcial (δ) del logaritmo natural de la ley de probabilidad estudiada.
Es decir, cuanto más probable sea una razón, menos datos transmite y viceversa. El ejemplo de un encabezado de periódico es representativo.
Cuando comienza con "Buenas tardes", la indagación se juzga como muy probable y transmite una cantidad de datos baja. Por el contrario, empezar con la tristemente célebre "Colombia en llamas", reviste una probabilidad baja y una cantidad de datos elevada, dirigida a hacer reaccionar a un gran número de espectadores.
15 - La formula PI
Esta formula es muy conocida ya que números como el PI lo conocemos desde el colegio. La ecuación de PI describe como la longitud de la circunferencia de un circulo, no varia cuando se relaciona al diámetro del mismo. El número PI equivale aproximadamente a 3.14.
PI nos ayuda a entender como funciona el campo de las coordenadas en un plano y como se hace funcionar el área de los GPS.
¿Cuál será la próxima innovación que nos puede mostrar la matemática? ¡En Superprof estaremos atentos y te lo contaremos!
¡Si deseas estudiar la función de un vector, la función de un eje, una recta o como encontrar un ángulo toma tu primer curso de matematicas, en Superprof, aquí encontraras los profesores adecuados para ti! Aprovecha que la primera clase es gratis.
Resumir con IA: