¿Eres de los que suma con los dedos o tiene que recurrir a una calculadora para contar devueltas?
Algunas operaciones son muy extensas para realizarlas en la cabeza, pero la mayor parte de las operaciones que necesitas resolver diariamente pueden hacerse sin necesidad de dispositivos o de tus manos. La matemática no es tan compleja como popularmente se piensa y se dice.
La agilidad que adquieras para realizar operaciones simples y otras un tanto más complejas te ahorrará mucho tiempo, además de proporcionarte agilidad mental y otro tipo de capacidades cognitivas que solo da el ejercicio del razonamiento lógico.
Existen muchos métodos que puedes implementar y algunos hábitos que puedes modificar o eliminar para mejorar en este y otros aspectos de las mates.
En este artículo, Superprof te presenta algunas recomendaciones para poner a funcionar tu inteligencia matemática.

¿Cómo aprender a derivar paso a paso?
Existen dos formas para lograrlo:
- Usando la definición de derivada.
- Usando las reglas de la derivación.
Lo primero para poder realizar la resolución de una operación de derivadas es conocer de límites, pues al terminar el derivar estas solo serán límites. También es importante que el estudiante tenga conocimientos, de álgebra y geometría, la primera de ellas, te va a ayudar a resolverlas de la operación que estás realizando, y la segunda te va a ayudar a entender mejor el concepto de derivada.
Cuando las derivadas existen, suelen determinar la pendiente de la línea tangente a una función, la cual también podremos conocerla como tasa de cambio, seguro la conoces, ya que esta última se usa para dar resolución a múltiples ejemplos matemáticos.
Para lograr determinar la pendiente debemos realizar el cálculo del límite.
Dicho de esta forma F‘(x) se deriva del punto P, normalmente aplicamos la siguiente fórmula.
f ‘(x) = lim f (x) – f (p)
Realizar el cálculo de los límites no representa un gran desafío, si están en funciones polinómicas de grados 2 o 3. Pues antes del límite de un polinomio, podremos realizar la resolución de los límites de cada monomio del cual se formó el polinomio.
Sin embargo, cuando las funciones polinómicas tienen un alto grado, también aumenta el grado de dificultad para conocer dichos límites. Entonces si queremos buscar una mayor agilidad, podremos probar los resultados posteriores, que en los cursos de matematicas medellin, veremos que generalmente se conocen como propiedades derivadas o las reglas de derivación.
¿Cuáles son los ejercicios combinados?
Es una ecuación numérica, en la que pueden aparecer varias operaciones, (adiciones, restas, multiplicaciones o divisiones). Estás puedes estar con o sin paréntesis.
Para dar resolución a una ecuación de estas, debemos tener en cuenta algunos factores, como la jerarquía de las operaciones, primero estarán las multiplicaciones, luego las divisiones, seguirán las adiciones y por último encontraremos las restas.
La ecuación combinada, algunas veces puede tener otros factores como los paréntesis, las llaves y los corchetes, aquí es cuando se hace necesario el PEMDSR, ahora a su vez podremos encontrar ejercicios en los que aparezcan fracciones básicas y exponentes, en el caso de estas se debe dar resolución al exponente después de los paréntesis y las en la fracción, primero se realizan las operaciones, sobre la barra que divide la fracción y luego la operación de abajo.
La matemática, es una ciencia que usamos día a día, y entonces ¿Por qué no aprenderla en clases de matemáticas Cali? Solicita tu primera clase gratis en Superprof.

¿Por qué es importante saber aplicar las mates?
Por que nos son útiles a diario, ya que nos enseñan sobre el equilibrio que deben conservar las proporciones en las construcciones y remodelaciones que hacemos a nuestros hogares, nos enseñan sobre la cantidades de ingredientes para hacer de cada receta un éxito, nos dan nociones de fracciones necesarias para dividir las tortas de cumpleaños de manera justa y suficiente, nos ayudan a calcular las dimensiones y equivalencias durante una mudanza y hasta ayudan a los estilistas en la medición de tintes para colorimetría y otros preparados.
Más allá de saber muchas fórmulas o memorizar conceptos de memoria, debemos saber cómo aplicar la matemática.
Padres, madres y docentes se quejan frecuentemente de que lo único que tienen que realizar los y las estudiantes es estudiar y aprenderse algunas cosas, pero que, de algún modo, los resultados reflejados en sus notas pueden no ser los esperados, además de los pocos conocimientos verificables obtenidos según su nivel.

El matemático italiano Bruno D’amore señala que esto puede atribuirse a que, aunque es verdad que tienen tiempo disponible para mates y otras materias, existe una desconexión casi que completa entre teoría y práctica. A los y las jóvenes se les puede llegar más fácil mostrándoles por qué es útil lo que les estás tratando de enseñar.
Muchas personas llegan a la edad adulta sin saber por qué memorizaron la mayor parte de los conocimientos que adquirieron en el colegio, pero todo lo que aprendemos tiene cierta aplicabilidad (o mucha) en el mundo real:
Saber sobre las transformaciones que ha sufrido el país en su historia y los cambios socioculturales derivados que han marcado nuestra historia debería permitirnos moldear nuestro criterio para tomar mejores decisiones y así no cometer los mismo errores en lo referente a la política;
Saber sobre biología nos debería poder enseñar sobre los beneficios que ofrecen diferentes especies de plantas y las costumbres de ciertas especies para así aprovechar los primeros y respetar las segundas; aprender sobre gramática debería enseñarnos que hay diferentes formas de comunicarse y nos debería dar las herramientas para transmitir los mensajes que queremos a llevar a los demás de la mejor manera.
El primer consejo –y el más importante, por cierto- para profesores y estudiantes es que busques la forma de aplicar los conocimientos a sus diferentes realidades para que sean más útiles y duraderos, y ¿qué mejor forma de realizar esto que haciendo tus cálculos que surjan al usar solo tu mente?
Beneficios de hacer cálculos en tu cabeza y no en tu calculadora:
Existen múltiples beneficios y posibilidades al realizar operaciones en tu cabeza:

- Desarrollas la memoria a corto plazo, uno de los factores determinantes para la inteligencia entendida como capacidad de razonamiento y aciertos en las respuestas.
- Desarrolla tu capacidad de diseñar estrategias y de planeación en diferentes áreas: existen varios juegos y ejercicios facilitan la capacidad de planeación, el pensamiento estratégico y abstracciones en diferentes situaciones de la vida.
- Favorece la agilidad mental: existe una relación muy fuerte entre entrenamiento matemático y la rapidez en las respuestas. Al igual que nuestros músculos, el cerebro necesita actividad constante para adquirir elasticidad y fuerza; la práctica de ejercicios matemáticos nos brinda una ligereza para realizar la resolución de otros ejercicios similar a la experimentada a las dos semanas de practicar cierto deporte.
Entonces, ¡empecemos a calcular!
¿Cuál es el orden que se deben resolver las operaciones?
Con el PEMDSR Paréntesis, exponentes, multiplicación y división de izquierda a derecha y adición y resta.
A grandes rasgos podríamos decir que lo primero que debemos es hacer la resolución de lo que tengan los paréntesis para lograra quitarlos y luego continuamos con los ejercicios de division y multiplicacion y por último estará la suma y la resta.
Reglas básicas de divisibilidad
- Dividir entre 2: es muy sencillo. Si el número es par (es decir, si termina en 2, 4, 6, 8 o 0) es divisible entre 2. Si por el contrario, es impar (termina en 1, 3, 5, 7 o 9) no es divisible entre 2.
Por ejemplo, el número 9658 puede dividirse entre 2 porque termina en 8; por el contrario, el número 9657 es impar y, por tanto, no puede dividirse entre 2.
- Dividir entre 4: si los dos últimos números de una cifra son divisibles entre 4, la cifras es divisible entre 4.
Lo que debes hacer es dividir primero entre 2 y luego otra vez entre 2.
Por ejemplo, para saber cuánto es 880 dividido entre 4, hacemos lo siguiente:
888 / 2 = 444
Y luego
444 / 2 = 222.
Como ves, con los dígitos del ejemplo lo que se hizo fue dividirlos entre 2 y listo, pero se puede realizar de la misma manera con números con mayor valor y diversos. Solo recuerda que sus dos últimas cifras deben ser, individualmente o en conjunto, divisibles entre 4.
- Dividir entre 3: una cifra se puede dividir entre 3 solo si la adición de los números que la componen es múltiplo de 3.
Tomemos un digitó grande como 6132: si los sumamos, el número resultante es 12. Luego sumamos esos dos dígitos y el resultado es 3, múltiplo de 3, por supuesto. Lo que debes recordar es realizar sumas de las cifras hasta reducirlas a un solo número y si recordar que sea múltiplo de 3 (es decir, 3, 6 o 9). - Divisibilidad entre 5: un dígito se puede dividir entre 5 si termina en 5 o en 0. Sin importar los números precedentes, lo importante es recordar que el último sea 5 o 0.
- Divisibilidad entre 10: esta es tal vez la menos compleja. Una cifra es divisible por 10 si termina en cero.
- Divisibilidad entre 11: Esta cuenta con un mayor extensión que las demás, pero es efectiva. Primero, para saber si un número es divisible entre 11, debemos ir al primer dígito de la cifra (el de la izquierda), y restar por duplas para luego restar los resultados de dichas operaciones. Suena enredado, pero seguro lo entiendes con el siguiente ejemplo:

- Tomemos la cifra 71995. Empezamos a armar duplas desde el primer dígito de la izquierda, es decir, 7:
(7, 1)(9, 9)(5)
No importa si queda un digitó sin pareja.
Luego restamos los dígitos contenidos en esos paréntesis, y si queda un dígito sin pareja, se deja como está:
(7-1)(9-9)(5)
Luego, sumamos estos resultados:
6 + 0 + 5 = 11
El 11 es múltiplo de 11, por supuesto y por lo tanto, es divisible entre 11.
Ahora bien, si se trata de una cifra compuesta por 3 dígitos, podemos realizar algo diferente. Se suma el primer y el tercer digitó y si da como resultado el digitó del medio, es divisible entre 11.
Tomemos la cifra 374:
3 + 4 = 7
Entonces, 374 es divisible entre 11.
Multiplicar por 11
Para multiplicar una cifra de 2 dígitos por 11, simplemente sumamos esos dos números y ponemos el resultante entre ellos, así:
Digamos que queremos realizar la multiplicación por 23 por 11:
2 + 3 = 5
Entonces,
23 x 11 = 253
Recuerda que solo funciona con cifras de tan solo dos dígitos.
Cómo sumar sin necesidad de calculadora
Uno de los trucos de mayor uso y menos complicados para realizar sumas y qué podemos aprender en clases de matematicas online es descomponer la cifra en unidades y decenas, y sumar los por separado como se muestra en el ejemplo:
Por ejemplo, si quieres saber cuánto es 74 (compuesto por 70 y por 4)+ 27 (compuesto por 20 y por 7)
Las unidades de estos dos dígitos son 4 y 7, y las decenas son 70 y 20, entonces, sumamos unidades con unidades y decenas con decenas. Luego sumamos los dígitos resultantes entre sí:
(70+20) + (7+4) = 90 + 11 = 101.

Intentemos con cifras un poco mayores
324 + 479:
Descomponemos así:
300 + 400 = 700
20 + 70 = 90
4 + 9 = 13
Luego
90 + 13 = 103
Entonces
700 + 103 = 803.
Cómo restar menos complicado
En un curso de matematicas bogota aprenderás que puedes restar de manera menos difícil si divides las cifras en bloques.
Por ejemplo, si quieres saber cuánto es 100 menos 37, ten en cuenta que 100 es 40 con una adición de 60, entonces
100 = 40 + 60
40 – 37 = 3
Le adicionas ese resultado a 60 y listo:
60 + 3 = 63
100 – 37 = 63
Operaciones con cada fracción
Las operaciones con fracciones son menos complejas de lo que parecen. Te explicamos la suma de los fraccionarios con un ejemplo. Digamos que quieres saber cuánto es un medio con una adición de dos tercios:
1 / 2 + 2 / 3
Primero, debes realizar la multiplicación en cruz y luego sumaremos, y ese será tu numerador (el digitó de arriba) y luego multiplicas los dígitos de abajo y ese será tu denominador, es decir.
(1 x 3) + (2 x 2) = 3 + 4 = 7
2 x 3 = 6
La respuesta es 7 / 6.
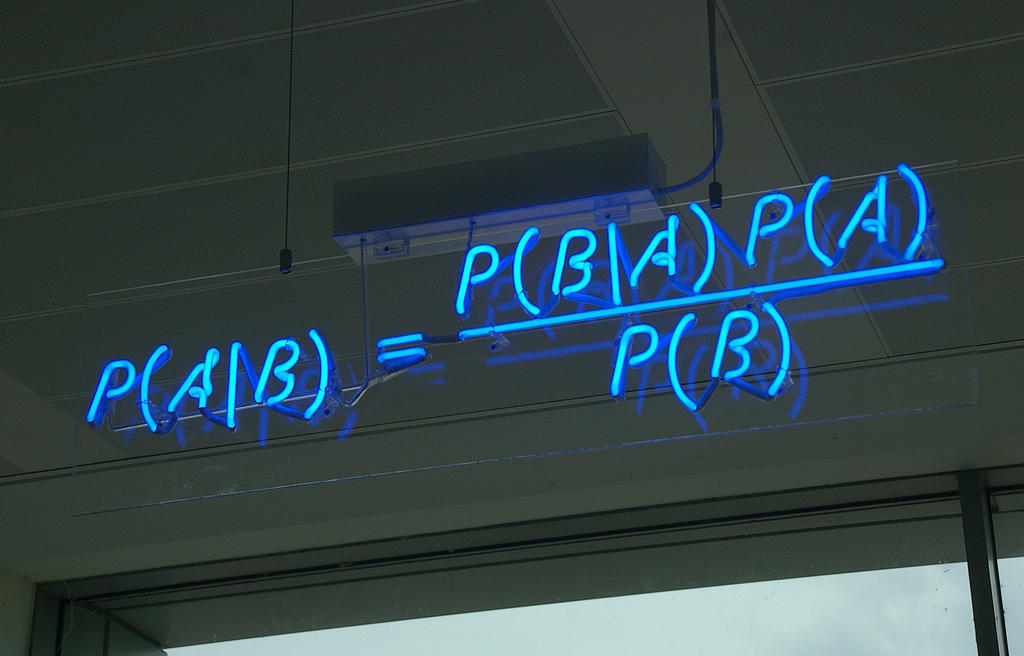
¿En qué situaciones podemos emplear el cálculo mental?
Pensamos que uno de los usos que tiene mayor frecuencia para estos trucos que acabamos de mostrarte son las pruebas de razonamiento lógico en la pruebas de ingreso a una universidad, tales como los exámenes para pasar a universidades públicas y privadas o las pruebas ICFES y Saber, pero su uso puede extenderse mucho.
La capacidad de realizar cuentas en tu cabeza te permite medir el tiempo con mayor facilidad (no solo las horas sino los años y los plazos), te permite calcular proporciones de productos, nos ayuda a mantener las cuentas claras con nuestro dinero y, en general, nos hace seres menos dependientes de la tecnología y con una mayor conexión a nuestras capacidades.
Por último, queremos recordarte que la destreza necesaria para llevar a cabo estas operaciones sin problemas es practicar y ser constante, y que articular estas claves con los conocimientos que recibes en un curso de matemáticas y en un curso de álgebra lineal, sin importar si son las del colegio, particulares presenciales o virtuales, definitivamente te darán una ventaja importante en ellas y en la vida diaria.
Después de todo, no se necesita realizar una operación mental muy elaborada para saber que la capacidad de hacer resolución de cada operación en tu cabeza es mejor que depender de tu teléfono inteligente.















